Introduction

Recently, I had to write a paper on a topic of interest for cryptography. Seeing how present cryptosystems rely on the hardness of problems such as factoring and discrete-logarithm, both of which are weak to Quantum Computers, I decided to investigate (attempts at) Post-Quantum Cryptography. In particular, I explored an early lattice-based cryptosystem known as the Goldreich-Goldwasser-Halevi (GGH) Encryption Scheme.

Continuing on from my paper, in this blog post I’ll be implementing both the cryptosystem itself, along with various attacks on it.

Background

Before we dive into the implementation, we will provide a quick recap of relevant concepts for the cryptosystem along with the high-level overview of the scheme itself.

Mathematical Prerequisites

First, we need to understand the notion of a “lattice” — after all, this is what the entire cryptosystem relies on for its security! Here, we define an $n$-dimensional lattice $\mathcal{L}$ to be an integer linear combination of vectors:

Another way to think of lattices is in terms of groups. Under a more group-theoretic perspective, lattices can be thought of as a group $\mathcal L$ satisfying the following two properties:

• Additive Subgroup
• Discrete: For each $g \in \mathcal L$, there exists an $\varepsilon$-neighborhood around them where there exists no other points.

Now, we call the set of linearly independent vectors which spans our lattice the basis. Notice that $\mathcal L$ can have infinitely many bases! An example of a lattice in the Euclidean plane can be seen below:

With this idea of bases, a natural question to ask is how we can differentiate between them. This is where the Hadamard Ratio comes in, which gives us a way to quantify the orthogonality of a chosen basis of $\mathcal L$:

The closer this ratio is to $1$, the more orthogonal our basis is. From the figure above, we see that for our example lattice $\mathcal L$, the basis $\left\{u_1, u_2 \right\}$ is more orthogonal than $\left\{v_1, v_2 \right\}$; i.e. the Hadamard Ratio of the former basis is higher than the latter.

The last key idea related to different lattice bases is that of unimodular matrices. A unimodular matrix $U$ is defined as a matrix with integer-valued entries with a determinant of $\pm 1$. As it turns out, for some unimodular matrix $U$ and basis $B$ of a lattice $\mathcal L$, the product $UB$ is also a basis for $\mathcal L$; the operation preserves the underlying lattice structure. Intuitively, we can think of unimodular matrices as acting like a change-of-basis matrix.

The Closest Vector Problem

With all of the mathematical prerequisites laid out, we can now discuss the crux of GGH’s security: the Closest Vector Problem (CVP). Loosely speaking, the idea is that, given a lattice $\mathcal L$ and some arbitrary vector $v \in V$ (not necessarily part of our lattice), we want to find the closest lattice point to said vector.

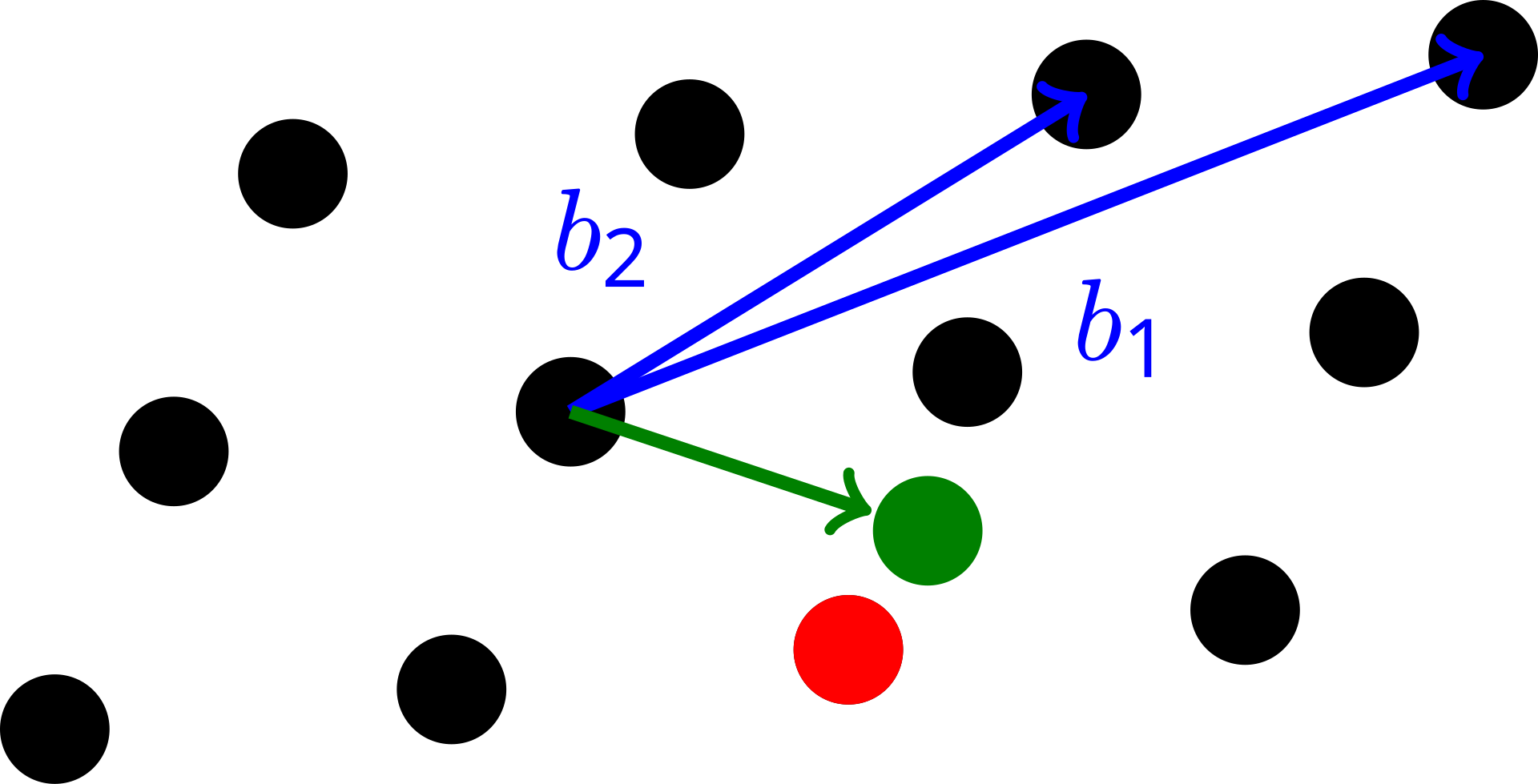
As it turns out, without knowing extra information like the basis of $\mathcal L$, it is very difficult to find this closest vector point! However, there exists algorithms that approximate CVP (such as Babai’s Rounding Technique) if the basis we work with is orthogonal enough (i.e. it has a high Hadamard Ratio). As such, it is clear how this could serve as the starting point for an encryption scheme.

The GGH Encryption Scheme

With all of this in mind, we now have the ingredients for the GGH Cryptosystem. First, we need to decide on the dimension $N$ of our lattice $\mathcal L$ and the “noise parameter” $\sigma$. Both of these values are pre-determined and public. In the original paper, the creators of GGH conjectured that a value of $N > 300$ and $\sigma = 3$ was sufficiently secure.

Next, since GGH is an asymmetric encryption method, we need a private and public key. For our private key, we will use a randomly-generated basis $K_{\mathrm{priv}}$ that has a high Hadamard Ratio (i.e. it is nearly orthogonal). This allows us to solve for CVP easily using methods like the aforementioned rounding technique.

For our public key, we can create a basis with a low Hadamard Ratio for our lattice by constructing some unimodular matrix $U$ and then constucting:

Because this basis has a low Hadamard Ratio, the rounding technique fails, and thus attackers — without knowing our private key — can’t decrypt our message.

From here, we describe the encryption and decryption process. For encryption, we will have an $N$-dimensional message vector $m$, whose entries are all integers. Next, we randomly generate a noise vector $e$, where each entry is picked randomly from the set $\left\{-\sigma, \sigma\right\}$. Then, we define our ciphertext $c$ as follows:

For the decryption process, suppose we’ve received some encrypted message $c$. Because we have knowledge of $K_{\mathrm{priv}}$ which has a high Hadamard Ratio, we can apply the rounding technique with this basis to eliminate the noise $e$. This yields us

From here, we can calculate the inverses of $K_{\mathrm{priv}}$ and $U$. Then, by right-multiplying, we get:

Thus, we’ve successfully recovered our message.

Implementing the Cryptosystem

Imports

First, we will be importing the following libraries:

import math
import numpy as np
import random

Helper Functions

Before implementing the encryption scheme, we will need to construct some helper functions first.

To begin with, we note that we will be communicating in a language like English. However, GGH represents messages using integer vectors. So, the question arises: how can we encode English into integers? A natural approach then is to use UTF-8 encoding , as seen below:

def encode(message: str) -> list[int]:
    encoded = message.encode("utf8")
    return np.array(list(encoded))

def decode(message: list[int]) -> str:
    message_bytes = bytes(message)
    return message_bytes.decode("utf8")

Now that we’ve implemented a way to convert our messages into integer vectors (and vice versa), we will want to implement a few other helper functions that will be used in our encryption scheme. Namely, we will implement the following:

• Babai’s Rounding Algorithm
• Unimodular Matrix Generation
• Hadamard Ratio Checker

def babai_round(basis: np.array , vec: np.array) -> np.array:
        # To begin with, we will want to express vec in terms of our private basis B.
        coeffs = np.linalg.solve(np.transpose(basis), vec)
        # Next, we round each coefficient in coeffs to the nearest integer.
        rounded_coeffs = np.round(coeffs)
        # Now, we find the resulting closest vector.
        rounded_vec = rounded_coeffs @ basis

        return rounded_vec

def check_basis(dimension:int, matrix:np.array) -> bool:
    if matrix is None:
        return False
    
    return np.linalg.matrix_rank(matrix) == dimension

def hadamard_ratio(dimension:int, matrix:np.array) -> float:
    if matrix is None:
        return -1
    
    _, log_determinant = np.linalg.slogdet(matrix)
    determinant = np.exp(log_determinant)
    norms = np.prod(np.linalg.norm(matrix, ord=2, axis=1))
    ratio = (determinant / norms)**(1 / dimension)
    return ratio

return unimodular @ private_key For checking if we have a valid basis, we can use the fact that it’s a basis if and only if it’s full rank (i.e. the rank of our matrix is equal to the dimension we are working in).

When verifying the Hadamard Ratio, due to how large our numbers can get, numpy can’t handle calculating the determinant without experiencing overflow. As a result, we instead use np.lingalg.slogdet() rather than just directly using np.linalg.det(). Unfortunately, there will be a recurring theme of running into integer overflows or rounding-errors later on… but for now, let’s continue with our implementation!

Naïve GGH

Now, we can start implementing the GGH cryptosystem. First, we will want to create a class for our GGH instance. As mentioned before, information that we will need are:

• dimension (int): The dimension we are working in.
• sigma (int): The value that we will use for our error vector.
• thresh (int): The value for each entry in our private key, from $[-\mathrm{thresh}, \mathrm{thresh}]$.

With that in mind, let us construct the class as follows:

from Utils.utils import Utils

class GGH:
    def __init__(self, dimension:int, sigma:int=3, thresh:int=4):
        self.dimension = dimension
        self.sigma = sigma
        self.thresh = thresh

        self.private_key = self.generate_private_key()
        self.unimodular = self.generate_unimodular()
        self.public_key = self.generate_public_key()

    def generate_private_key(self) -> np.array:
        ...
    
    def generate_unimodular(self) -> np.array:
        ...
    
    def generate_public_key(self) -> np.array:
        ...
    
    def encrypt(self, message:str) -> np.array:
        ...
    
    def decrypt(self, ciphertext:np.array) -> str:
        ...

We will now have to implement our key generation, which involves writing up code to generate our private key $K_{\mathrm{priv}}$, a random unimodular matrix $U$, and our public key $K_{\mathrm{pub}}$. First, we implement generating a private key as such:

def generate_private_key(self) -> np.array:
    basis = None
    while (not Utils.check_basis(dimension, basis)) or (Utils.hadamard_ratio(dimension, basis) < 0.75):
        vecs = []
        for _ in range(dimension):
            vec = []
            for _ in range(dimension):
                vec.append(random.randint(-thresh, thresh))
            vecs.append(vec)
        
        basis = np.array(vecs)

    return basis

Here, the idea is that we construct a random basis $K_{\mathrm{priv}}$ that has a good-enough Hadamard ratio (in this case, we arbitrarily picked one of at least $0.75$).

Next, we generate our public key. This involves first genreating our unimodular $U$, and then multiply our private key by it:

def generate_unimodular(self, iters:int=-1) -> np.array:
    identity = np.eye(self.dimension, dtype=int)
    if iters == -1:
        iters = self.dimension**2

    for iter in range(iters):
        operation = random.randint(0, 2)
        i = 0
        j = 0
        while i == j:
            i = random.randint(0, dimension-1)
            j = random.randint(0, dimension-1)

        if operation == 0:
            identity[[i, j]] = identity[[j, i]]
        elif operation == 1:
            multiplier = random.choice([-1, 1])
            identity[i] *= multiplier
        else:
            identity[i] += identity[j]
        identity = identity.astype(int)

    return identity

def generate_public_key(self) -> np.array:
    return self.unimodular @ self.private_key

For generating a unimodular matrix, we can start with the $n \times n$ identity matrix $I$. Then, for some number of iterations iters, we randomly select one of three operations to perform:

• Row Swap
• Row Scaling (by $1$ or $-1$)
• Row Addition

The idea then is that these operations will preserve the determinant of our identity matrix, and retains integer entries; thus, a unimodular matrix $U$ will be formed.

Now, all that is left is to actually encrypt and decrypt our messages following the GGH scheme:

def encrypt(self, message:str) -> np.array:
    encoded = Utils.encode(message)
    error_vector = Utils.generate_error(self.dimension, self.sigma)
    ciphertext = encoded @ self.public_key + error_vector
    return ciphertext
    
def decrypt(self, ciphertext:np.array) -> str:
    closest_vector = Utils.babai_round(self.private_key, ciphertext)
    message = np.round(closest_vector @ np.linalg.inv(self.private_key) @ np.linalg.inv(self.unimodular))
    return Utils.decode(message.astype(int))

Thus, we have coded up a basic implementation of GGH. Finally, to check if it is working, we can try encrypting and decrypting a message:

message = "hello!"
dim = len(message)
inst = GGH(dimension=dim)
encrypted = inst.encrypt(message)
decryptyed = inst.decrypt(encrypted)

print("Message:", message)
print("Encrypted:", encrypted)
print("Decrypted:", decryptyed)

And this gives us the following output:

>Message: hello!
>Encrypted: [ 11548  81154  60556 -55448  48826 -43009]
>Decrypted: hello!

Issues

However, while our implementation works right now, there are some glaring issues. To begin with, we start running into decryption errors with dimensions as low as $n \approx 80$. Keep in mind, this scheme is conjectured to need at least $n > 400$ for it to be secure against currently-known attacks! This stems from, as we’ve foreshadowed before, rounding errors due to how numPy does arithmetics. Namely, let us consider the following message:

>Message: hello! how are you? i am honestly kind of tired today, but i hope you are well!
>Encrypted: [-209819066574 -131587654269   ...  -90926829761   96783511052]
>Decrypted: hello! hovare yov? i am honestly lind of tired todaz+ but i hope yov are well!

When encrypting/decrypting, we get:

Another issue is it takes a very long time when working with higher dimensions; this problem can be resolved a lot easier. For this, it’s mostly due to the fact that the algorithms we use for generating the private key and unimodular matrix could be improved upon. We will be referring to the algorithms outlined in the original GGH paper for constructing these two things.

Improving the Implementation

With all of that in mind, we first want to extend our implementation to accurately handle higher-dimension situations. Luckily, the FLINT and symPy libraries prove to be especially helpful for this endeavor. However, there is a small trade-off between accuracy and speed.

First, we will be needing a helper function to convert between numPy (or symPy) arrays and the fmpz matrices from FLINT. We will also rewrite the check_basis() function to instead simply check whether or not the determinant is non-zero:

class Utils:
    # ...

    def conv_to_fmpz(array):
        return fl.fmpz_mat([[int(item) for item in sublist] for sublist in array.tolist()])

    def check_basis(matrix:fl.fmpz_mat) -> bool:
        if matrix is None:
            return False
        
        return matrix.det() != 0

We will also re-write our functions for generating the private key $K_\mathrm{priv}$ and unimodular matrix $U$:

class GGH:
    # ...

    def generate_private_key(self) -> fl.fmpz_mat:
        k = fl.fmpz(self.thresh * math.ceil(math.sqrt(self.dimension)))
        identity = Utils.conv_to_fmpz(np.eye(self.dimension))
        basis = None
        while not Utils.check_basis(basis):
            r = fl.fmpz_mat([[random.randint(-self.thresh, self.thresh) for _ in range(self.dimension)] for _ in range(self.dimension)])
            basis = r + (k * identity)

        return fl.fmpz_mat(basis)

    def generate_unimodular(self, iters:int=2) -> fl.fmpz_mat:
        x = sp.zeros(1, self.dimension)
        identity = sp.eye(self.dimension)

        weights = [1, 5, 1]
        vals = [-1, 0, 1]

        for _ in range(iters):
            rows = list(range(dim))
            random.shuffle(rows)
            for i in rows:
                x[0, i] = 1
                for j in range(self.dimension):
                    if j != i:
                        x[0, j] = random.choices(vals, weights=weights)[0]

                new_row = x * identity
                for j in range(dim):
                    identity[i, j] = new_row[0, j]
                
                x[0, i] = 0
        
        return Utils.conv_to_fmpz(identity)
    
    # ...

Then, with some small tweaks to our previous functions to accomodate the switch to FLINT, we have successfully transformed our implementation so that it can handle larger dimensions! For example, let us try encrypting the start of my favorite poem, The Raven :

>Message: Once upon a midnight dreary, while I pondered, weak and weary, Over many a quaint and curious volume of forgotten lore- While I nodded, nearly napping, suddenly there came a tapping, As of some one gently rapping, rapping at my chamber door. 'Tis some visitor,' I muttered, 'tapping at my chamber door- Only this and nothing more.'
>Encrypted: [-5353784417535089015376456486595758  4464135996091873026654645932943924  ...  2299615342658008421305325526349  3012616251689126733682718467252442]
>Decrypted: Once upon a midnight dreary, while I pondered, weak and weary, Over many a quaint and curious volume of forgotten lore- While I nodded, nearly napping, suddenly there came a tapping, As of some one gently rapping, rapping at my chamber door. 'Tis some visitor,' I muttered, 'tapping at my chamber door- Only this and nothing more.'